CylinderAreaParadox
N.B. Le texte de Bachelard dans la section ci-dessus utilise la lettre n pour désigner le nombre de plans et la lettre m pour le nombre de sommets. Dans le texte ci-dessous n donne le nombre de sommets et m le nombre de plans.
Let 
be the surface of a cylinder of height 
and radius 
. (
does not include the flat circular ends of the cylinder.) This
Demonstration constructs a set of triangles that tend uniformly to —yet their total area does not tend to the area of !
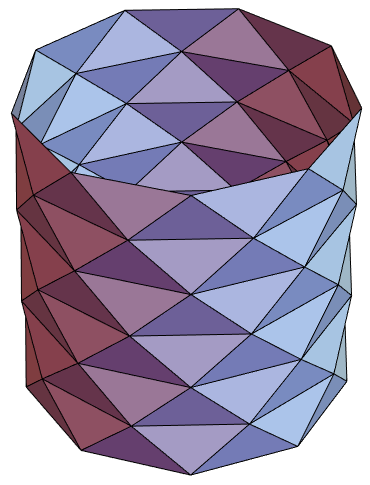
Divide into 
subcylinders (or bands) of height 
. Construct 
congruent isosceles triangles in each band with vertices at the vertices of a regular -gon inscribed in the circles at the top and bottom of each band, offset by 
.
For any point 
in 
(except the axis of the cylinder), let 
be the axial projection of onto . As 
, to say that the triangles approximate uniformly means that for any point 
on a triangle and any 
(independent of ), there is a 
such that for all 
, 
.
The sum of the areas of the triangles is
.
Depending on how the limit is taken, 
can differ. If first 
with held fixed and then 
, the limit is 
, the expected area of the cylinder. If first with 
held fixed and then , the limit is infinity. If and together so that 
is some positive constant 
, the limit can be chosen to be any number greater than .
Therefore 
does not have a limit.
The surface is known as Schwarz's lantern, Schwarz's polyhedron, or Schwarz's cylinder.
George Beck and Izidor Hafner
"Cylinder Area Paradox"
http://demonstrations.wolfram.com/CylinderAreaParadox/
Wolfram Demonstrations Project