Aperçu des sections

  • Généralités

    Tout replier Tout déplier
    MSN 21 : Poser et résoudre des problèmes pour structurer le plan et l'espace
    • en dégageant des propriétés géométriques des figures planes et en les classant
    • en dégageant des propriétés des solides et en s’initiant à leur représentation
    • en représentant des figures planes et des solides à l’aide de croquis, de maquettes, d’ébauches de perspective,…
    • en effectuant des isométries et en décrivant des déplacements à l’aide d’isométries
    • en s’appropriant et en utilisant des systèmes conventionnels de repérage
    • en utilisant des instruments de géométrie

    N. B. Pour utiliser les mini-applications dans les sections ci-dessous, vous devez installer Wolfram CDF Player sur votre poste.

  • Section 1

    Essai sur la connaissance approchée

    Gaston Bachelard
    Librairie philosophique J. Vrin
    3e édition, Paris 1969

    Illustration d'un extrait
    p. 170
    «On peut montrer par de nombreux exemples que l'intuition mathématique est impropre à l'analyse qui conduit à une connaissance rigoureuse.  En voici un, indiqué jadis par Schwartz, et qui ne paraît pas avoir frappé les philosophes. Rien de si intuitif que la surface qui enveloppe un corps. Son évaluation mathématique par le calcul intégral peut présenter  des difficultés techniques considérables, elle ne paraît cependant mettre en jeu que des idées simples; on remplace la surface par des éléments du plan tangent, on détermine ainsi une intégrale qu'il n'y a qu'a effectuer pour avoir le résultat. Mais l'intuition eût tout aussi bien accepté une méthode différente. Prenons trois points rapprochés de la surface, ils déterminent un plan qui peut être aussi voisin qu'on veut de l'élément de surface. On peut ainsi constituer une infinité de facettes planes dont la somme intégrale devra à la limite, semble-t-il donner la surface cherchée.
    Cette méthode peut cependant être illusoire. Pour le montrer, Schwartz considère un cylindre circulaire droit dont la surface latérale est, comme on le sait, égale à 2\( \pi \)rh, et il propose de la calculer de la manière suivante. Coupons le cylindre en n cylindres partiels par des plans équidistants perpendiculaires à l'axe.»
    Cylindre coupé en n cylindres partiels par des plans équidistants perpendiculaires à l'axe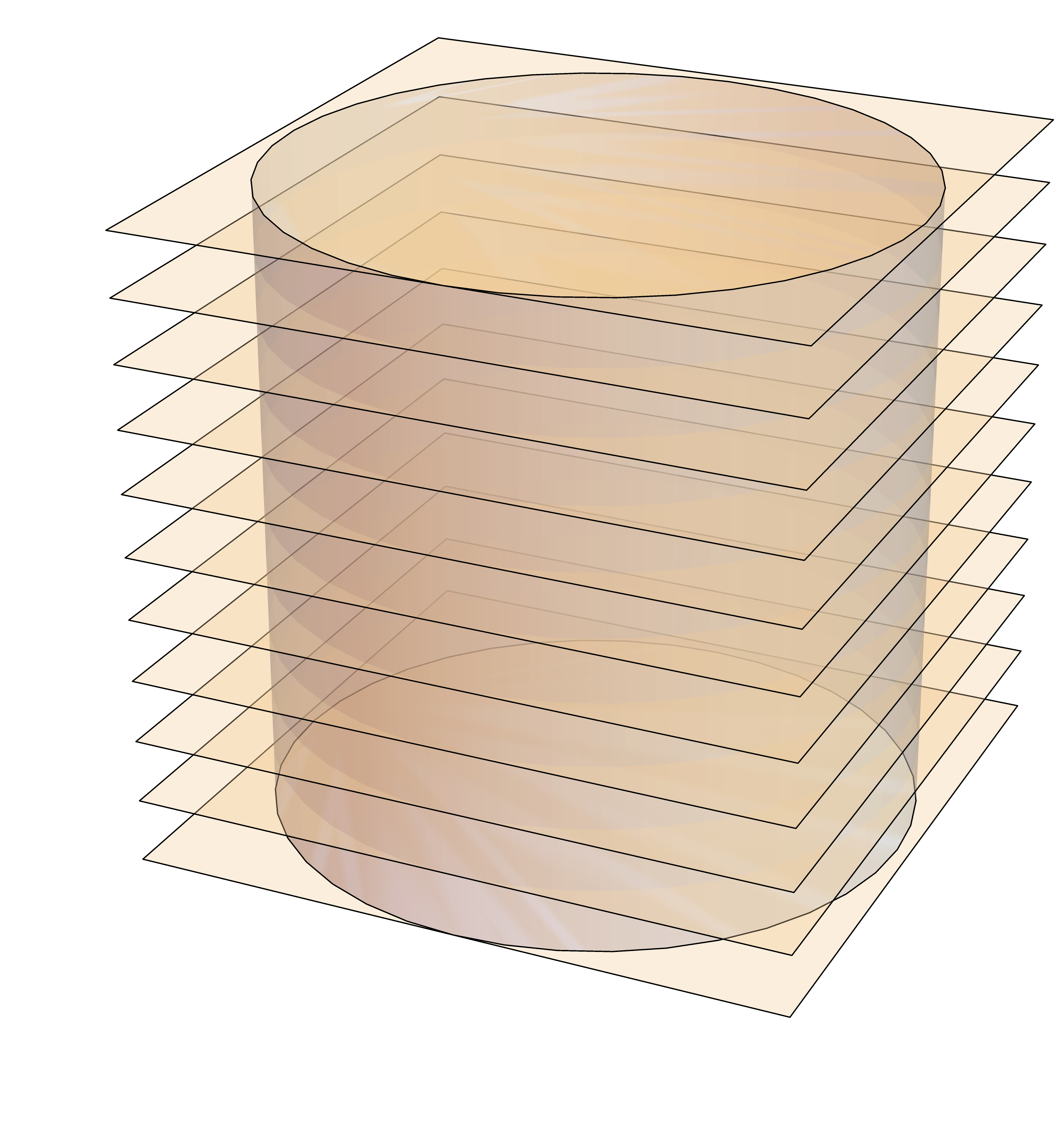
    «Sur chaque circonférence de section, choisissons des points situés au sommets d'un polygone régulier de m côtés et de telle façon que les sommets d'un polygone soient à égale distance des sommets du polygone immédiatement inférieur.»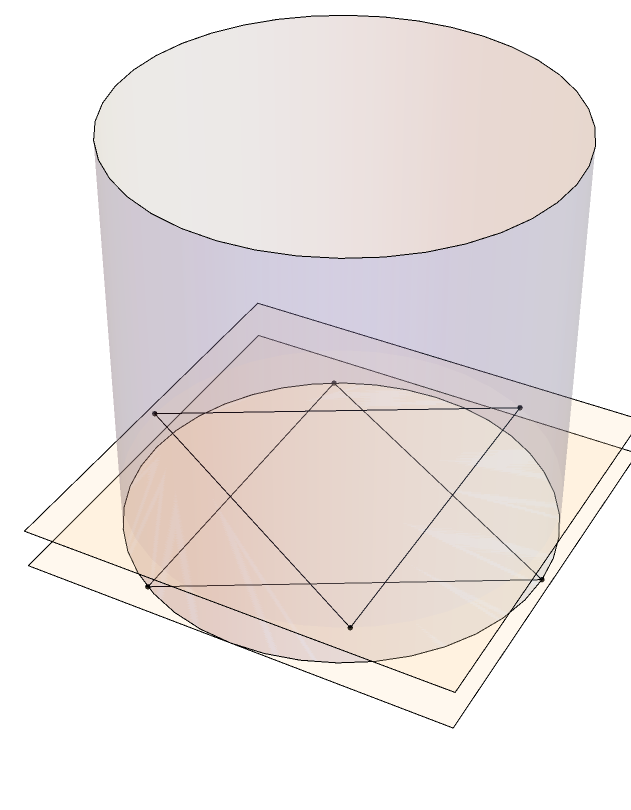
    Points au sommets d'un polygone régulier de m côtés dont les sommets sont à égale distance des sommets du polygone inférieur
    «En reliant chaque point d'une section aux deux points les plus proches de la section voisine, on obtient des triangles isocèles.»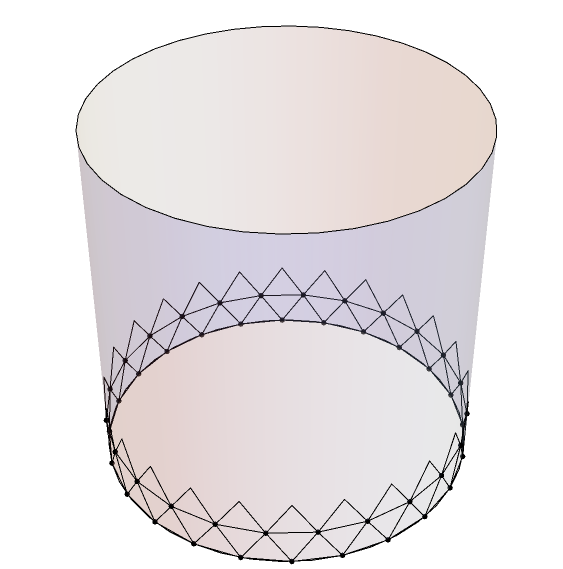
    Chaque point d'une section est relié aux deux points les plus proches de la section voisine
    «Cherchons la surface des triangles isocèles ainsi formés. Leur base est égale à :
    \( 2 r \sin \left(\frac{\pi }{m}\right) \)

    leur hauteur, aux infiniment petits près du troisième ordre :
    \(\sqrt{\frac{h^2}{n^2}+\frac{\pi ^4 r^2}{4 m^4}} \)
    La superficie d'un petit triangle est donc :
    \( r \sin \left(\frac{\pi }{m}\right) \sqrt{\frac{h^2}{n^2}+\frac{\pi ^4 r^2}{4 m^4}} \)
    et comme il y en a 2mn, la surface polyédrique inscrite peut être mise sous la forme :
    \( 2 mnr \sin \left(\frac{\pi }{m}\right) \sqrt{\frac{h^2}{n^2}+\frac{\pi ^4 r^2}{4 m^4}} \)
    ou encore, en confondant le sinus avec l'angle :
    \( 2\pi nr \sqrt{\frac{h^2}{n^2}+\frac{\pi ^4 r^2}{4 m^4}} \)
    Resterait à faire tendre n et m vers l'infini. On devrait, semble-t-il, retrouver la formule classique. Mais la somme intégrale dépend ici de la façon dont se comporte le rapport \( n / m^2 \) à la limite. On voit alors que la limite de la surface polyédrique peut prendre n'importe quelle valeur supérieure à la valeur réelle, si l'on reste libre de l'accroissement séparé des points de division du cercle et des plans de section. Pour retrouver la formule élémentaire, il faut faire tendre vers l'infini séparément n et m, mais de telle manière que \( n / m^2 \) tende vers 0.»
    \( \underset{n\to \infty }{\text{lim}}\underset{m\to \infty }{\text{lim}}2 \pi r \sqrt{h^2+\frac{\pi ^4 n^2 r^2}{4 m^4}} \)
    • url icon
      CylinderAreaParadox URL

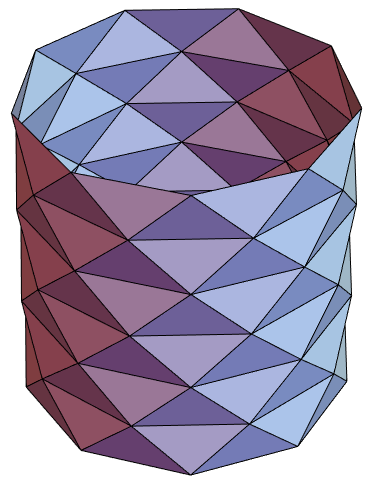
      Lanterne de Schwartz

      N.B. Le texte de Bachelard dans la section ci-dessus utilise la lettre n pour désigner le nombre de plans et la lettre m pour le nombre de sommets. Dans le texte ci-dessous n donne le nombre de sommets et m le nombre de plans.

      Let be the surface of a cylinder of height and radius . ( does not include the flat circular ends of the cylinder.) This Demonstration constructs a set of triangles that tend uniformly to —yet their total area does not tend to the area of !

      Divide into subcylinders (or bands) of height . Construct congruent isosceles triangles in each band with vertices at the vertices of a regular -gon inscribed in the circles at the top and bottom of each band, offset by .

      For any point in (except the axis of the cylinder), let be the axial projection of onto . As , to say that the triangles approximate uniformly means that for any point on a triangle and any (independent of ), there is a such that for all , .

      The sum of the areas of the triangles is

      .

      Depending on how the limit is taken, can differ. If first with held fixed and then , the limit is , the expected area of the cylinder. If first with held fixed and then , the limit is infinity. If and together so that is some positive constant , the limit can be chosen to be any number greater than .

      Therefore does not have a limit.

      The surface is known as Schwarz's lantern, Schwarz's polyhedron, or Schwarz's cylinder.

      George Beck and Izidor Hafner "Cylinder Area Paradox"
      http://demonstrations.wolfram.com/CylinderAreaParadox/
      Wolfram Demonstrations Project